|
SME Light Winter Quarter Lecture 8: How Do We Describe Symmetry? Thursday, January 27th, 2000 Outline
I. Symmetry elements (Cn, s, Sn) and symmetry operations Materials needed:
BREAK-OUT SESSION: What do you think "symmetry" is? Write down your thoughts on the index cards and don't forget to write your name. We'll put a list of peoples' definitions up on the web. BREAK-OUT SESSION: Show a physical model of something triangular and something tetrahedral. Which is "more symmetric?" Justify your answer on your index card. The tetrahedron is considered more symmetric because there are more "symmetry operations" that you can do on the tetrahedron that leave it unchanged. We will talk about exactly what these are soon. Another way to put this is that the tetrahedron has more "symmetry elements." What are symmetry operations and elements?? I. Symmetry elements (Cn, s, Sn) and symmetry operations Symmetry elements are the lines or planes about which we can rotate or reflect a figure such that it appears unchanged after the operation is over. We can rotate a figure around an n-fold rotation axis (Cn) or reflect the figure through a mirror plane (s). If we rotate the figure 360/n degrees around a Cn axis and then reflect it through a plane perpendicular to that axis, we say that we have done an n-fold improper rotation (Sn). Think of some examples of each kind of symmetry operation: Cn, s, and Sn. Symmetry operations are the acts of rotating or reflecting a molecule about one of its symmetry elements. If we say that a molecule has symmetry C4 about a given axis, we mean that 4 equal rotations (of 90 degrees each) about that axis will get us back to where we started, and that each of the four rotations will leave the molecule in a position identical to its starting position. A simply test can be done to determine whether a symmetry operation is indeed valid. Close your eyes, have someone do the operation, and then see if you can tell that a change has been made. If you can't, then the symmetry operation was valid. BREAK-OUT SESSION: Where are the symmetry elements in the figure below (rotation axes, mirror planes, improper rotation axes)? How many ways can you rotate or reflect it so that it is unchanged (i.e. how many symmetry operations does it have)?
 Symmetry elements: This figure has 7 mirror planes: 6 perpendicular to the page (s) and 1 in the plane of the paper (s'). There is a 6-fold rotation axis (C6) perpendicular to the plane of the paper that also contains 3-fold and 2-fold rotation axes (C3 and C2). All of these contain improper rotation axes as well, because reflecting the figure through the plane of the paper does not affect how how the figure appears. There are six 2-fold rotation axes (C2')in the plane of the paper. These do not contain improper rotation axes. Symmetry operations: There are a lot of symmetry operations for this figure! You can do six different operations about the C6 axis, 3 about the C3 axis, etc. Look at a physical model of the tetrahedron. Find all of the symmetry elements of the tetrahedron. Note that tetrahedra will be particularly important for us later when we talk about chirality and the tetrahedral geometry of the carbon atom. Symmetry elements of a tetrahedron (can you find them all?): three 2-fold rotation axes (C2) perpendicular to each other, four 3-fold rotation axes (C3), six mirror reflection planes (s), and three 4-fold improper rotation axes (S4) containing the 2-fold rotation axes. Sometimes the C3 axes are difficult to see. Check out the online version of these notes to see an interactive version that might help you see the C3 axes better! BREAK-OUT SESSION: One common way to think about symmetry is to think about "inversion," or taking every point in the figure through a point in the center and out the other side to see if the figure is changed or unchanged. But we didn't mention inversion here. Why don't inversion centers "count" as symmetry elements? An inversion center allows you to perform an operation that has the same effect as an S2 axis!! II. Point groups A point group is a name for a collection of symmetry elements which are commonly found together in the same figure. A compound which has all of the symmetry elements of a point group is said to "belong" to that point group. Following is a listing of some of the common symmetry elements for various point groups and a "decision tree" that you can use to help you decide what point group any given element belongs in. III. The decision tree Below is the "decision tree," a pictoral representation of how you can put molecules in point groups. Don't try to memorize the decision tree; it will always be provided for you. But if you prefer to think about these things in a non-pictoral way, here's a textual description: There are four sets of point groups. The first is for molecules with low symmetry: C1 (only E), Cs (only E and sigma), and Ci (only E and I). The second is for molecules with high symmetry: Td, (tetrahedral), Oh (octahedral), and Ih (icosohedral). If a molecule doesn't fall into the low symmetry groups or the high symmetry groups, then it is in either one of the Cn groups or the Dn groups. The difference is that a molecule in a Dn group has n C2 axes perpendicular to the principle axis, where n is the order of the principle axis. The subscripts are as follows: if there is a sigma h (perpendicular to the principle rotation axis), add an h; if there is no sigma h but a sigma v (containing the principle rotation axis), add a v; if there are no reflection planes, don't add a subscript. One more rule: there is no such thing as a Dnv point group, so if you have this, call it instead a Dnd molecule. The official definition is that if the v planes bisect C2 axes, then these are dihedral reflections, and are denoted d. The Decision Tree itself is below.
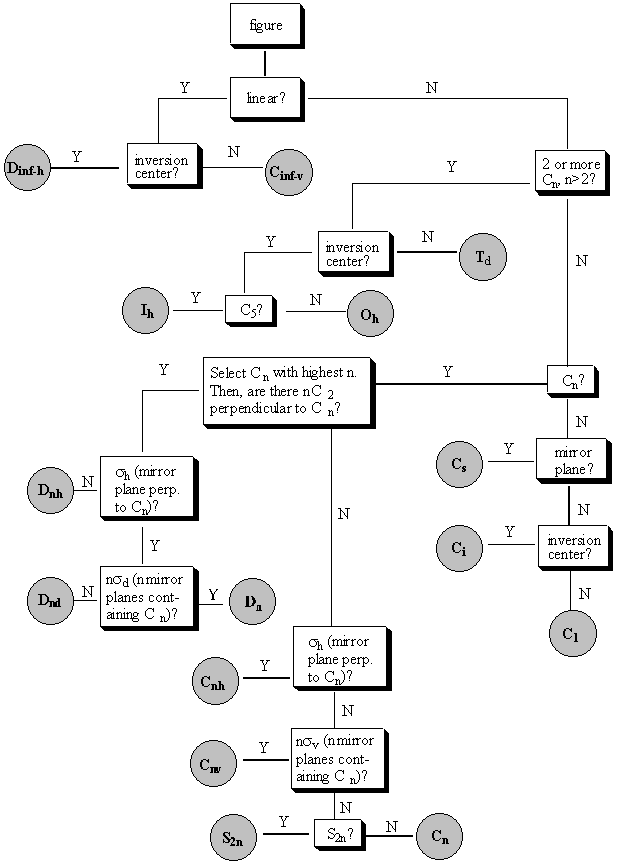 Go through the decision tree for the six-pointed star we considered at the beginning of lecture. Follow along below to see how it helps you to assign the point group.
Question: linear? Answer: no Point group: D6h The only way to really understand point groups is to get lots of practice. Go to the web and use the online lecture notes. Move them around with the mouse and look at them from different angles to make sure you don't miss any of their symmetry elements. Some of them are very difficult! When you get the hang of it, this can be fun (in a sick sort of way . . .). You may find yourself unable to stop assigning point groups; to leaves, to window panes, to your elevator door and Brad's eyeglasses . . .
|